Hello Stan!

In my previous post I discussed how Longley-Cook, an actuary at an insurance company in the 1950’s, used Bayesian reasoning to estimate the probability for a mid-air collision of two planes.

Here I will use the same model to get started with Stan/RStan, a probabilistic programming language for Bayesian inference.

Last week my prior was given as a Beta distribution with parameters \(\alpha=1, \beta=1\) and the likelihood was assumed to be a Bernoulli distribution with parameter \(\theta\): \[\begin{aligned} \theta & \sim \mbox{Beta}(1, 1)\\ y_i & \sim \mbox{Bernoulli}(\theta), \;\forall i \in N \end{aligned}\]For the previous five years no mid-air collision were observed, \(x=\{0, 0, 0, 0, 0\}\). That’s my data.

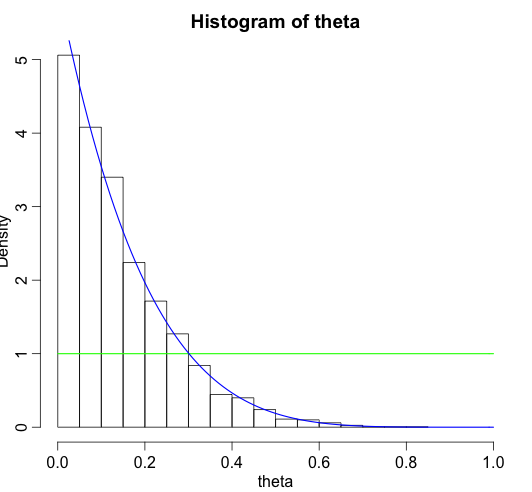
In this case the posterior distributions can be derived analytically. The posterior hyper-parameters are \(\alpha'=\alpha + \sum_{i=1}^n x_i,\, \beta'=\beta + n - \sum_{i=1}^n x_i\) and with that I get the posterior parameter for the predictive distribution, which is a Bernoulli distribution again: \(\theta' = \alpha'/(\alpha'+\beta')=\frac{1}{7} \approx 14.3\)%.

Still, I can use Stan and MCMC simulations to come to the same answers (of course I am using a sledgehammer here to crack a nut).

In the first code block the model is written in Stan’s modelling language. The next section calls stan and finally the results can be analysed. The answers are very much the same as the analytical approach in my previous post.

Interested in the application of R in insurance? Join us at the 3rd R in Insurance conference in Amsterdam, 29 June 2015.

Session Info

R version 3.2.0 (2015-04-16)
Platform: x86_64-apple-darwin13.4.0 (64-bit)
Running under: OS X 10.10.3 (Yosemite)

locale:
[1] en_GB.UTF-8/en_GB.UTF-8/en_GB.UTF-8/C/en_GB.UTF-8/en_GB.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] rstan_2.6.0   inline_0.3.14 Rcpp_0.11.6  

loaded via a namespace (and not attached):
[1] tools_3.2.0      codetools_0.2-11 stats4_3.2.0