Measuring temperature with my Arduino

It is really getting colder in London - it is now about 5°C outside. The heating is on and I have got better at measuring the temperature at home as well. Or, so I believe.

Last week’s approach of me guessing/feeling the temperature combined with an old thermometer was perhaps too simplistic and too unreliable. This week’s attempt to measure the temperature with my Arduino might be a little OTT (over the top), but at least I am using the micro-controller again.

Yet, I have to overcome similar challenges again as last week. The Arduino with the temperature sensor (TMP36) should be a better device to measure the temperature than my thermometer, but it isn’t perfect either and the readings will have some uncertainty as well. But, it will be easy to make frequent measurements and with a little trick I should be able to filter out the noise and get a much better view of the ‘true’ temperature.

The trick is Bayesian filtering, or as it turns out, a simplified Kalman filter (univariate, no control actions, no transition matrices).

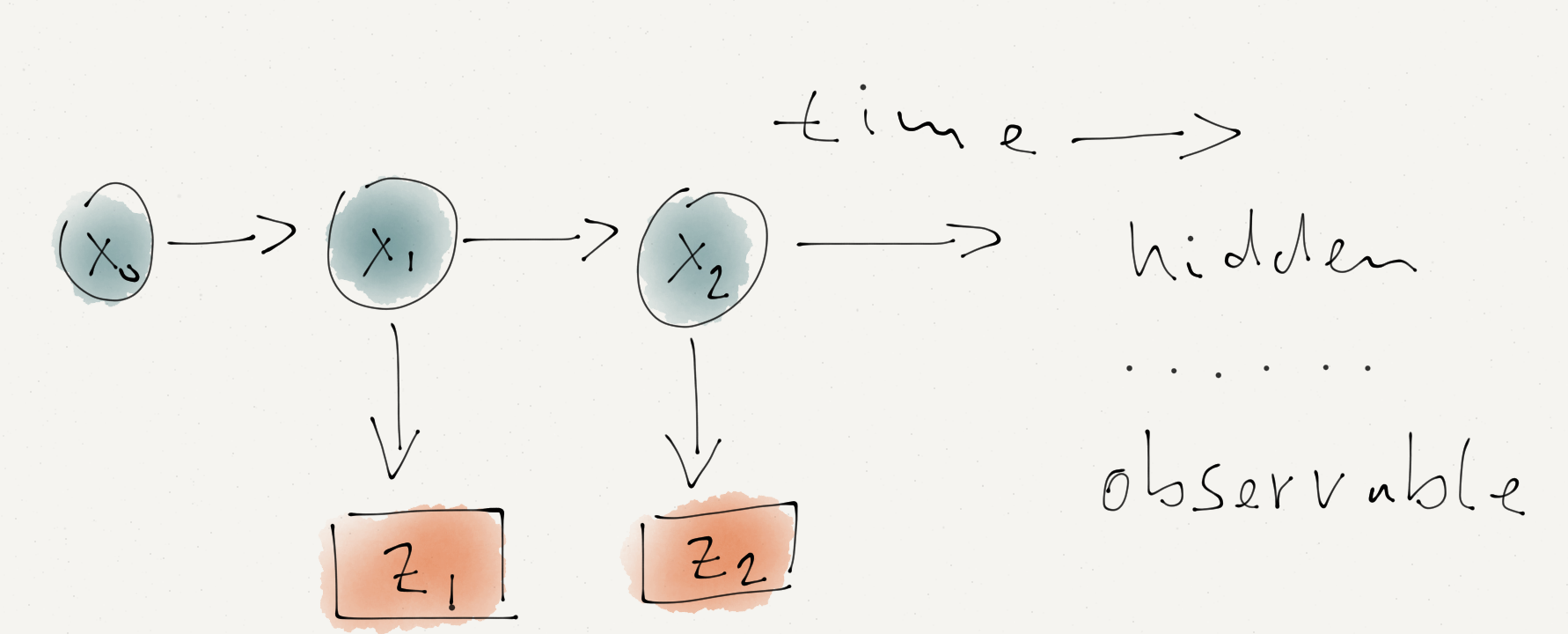
I can’t observe the temperature directly, I can only try to measure it. I think of this scenario as a series of Bayesian networks (or Hidden Markov Model). The hidden or latent variable is the ‘true’ temperature and the observable variable is the reading of my Arduino sensor.

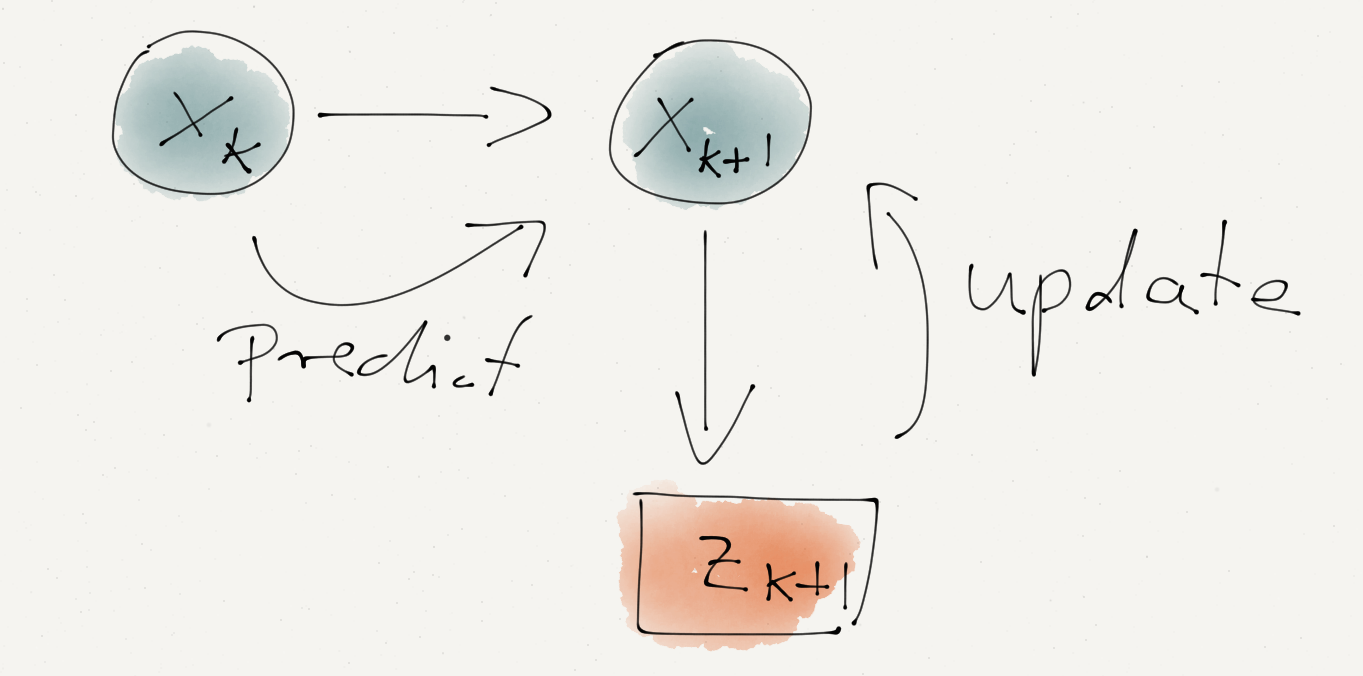
I start with a prior guess of the Temperature at time \(k=0\), just like last week (note, here I will use \(x_k\) instead of \(\mu_k\)). My initial prior is \(N(x_0, \sigma_0^2)\). Now I predict the state (temperature) \(\hat{x}_1\) at the next time step. I expect the temperature to be largely unchanged and therefore my prediction is just \(\hat{x}_1 = x_0 + \varepsilon_P\) with \(\varepsilon_P \sim N(0, \sigma_P^2)\) describing the additional process variance going from one time step to the next. The process variance is independent from the uncertainty of \(x_0\), hence I can add them up and thus my prior for \(x_1\) is \(N(x_0, \sigma_0^2+\sigma_P^2)\).

The measurement of the temperature should reflect the ‘true’ temperature with some measurement uncertainty \(\sigma_M\). My prediction of the measurement is \(\hat{z}_1 = \hat{x}_1 + \varepsilon_M\) with \(\varepsilon_M \sim N(0, \sigma_M^2)\). The best estimator for \(\hat{z}_1\) is the actual measurement \(z_1\) and therefore the likelihood distribution of \(z_1|x_1\) is \(\,N(z_1, \sigma_M)\). Applying the formulas for Bayesian conjugates again gives the hyper-parameters for the posterior normal distribution \(x_1|\,z_1, x_0\), the temperature given the measurement and my prediction from the previous time step:

\[ \begin{aligned} x_1&=\left.\left(\frac{x_0}{\sigma_0^2+\sigma_P^2} + \frac{z_1}{\sigma_M^2}\right)\right/\left(\frac{1}{\sigma_0^2+\sigma_P^2} + \frac{1}{\sigma_M^2}\right) \\ \sigma_1^2 & =\left(\frac{1}{\sigma_0^2+\sigma_P^2} + \frac{1}{\sigma_M^2}\right)^{-1} \end{aligned} \] With \[ K_1 := \frac{\sigma_0^2+\sigma_P^2}{\sigma_M^2+\sigma_0^2+\sigma_P^2} \]

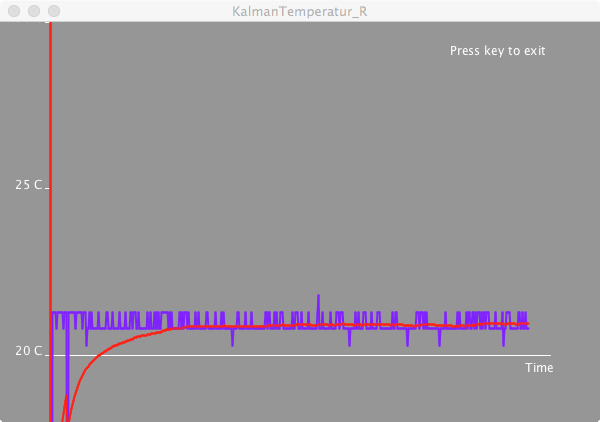
this simplifies to: \[ \begin{aligned} x_1 & = K_1\, z_1 + (1 - K_1)\, x_0\\ \sigma_1^2 & = (1 - K_1) (\sigma_0^2 + \sigma_P^2) \end{aligned} \] This gives the simple iterative updating procedure (or Kalman filter): \[ \begin{aligned} K_{k+1} & = \frac{\sigma_k^2+\sigma_P^2}{\sigma_M^2+\sigma_k^2+\sigma_P^2} \\ \sigma_{k+1}^2 & = (1 - K_{k+1}) (\sigma_k^2 + \sigma_P^2)\\ x_{k+1} & = K_{k+1}\, z_{k+1} + (1 - K_{k+1})\, x_k \end{aligned} \] In my code below I set the process variance to \(\sigma_P^2=0.01\) and the measurement variance to \(\sigma_M^2=0.5\), which led to a fairly stable reading of 21.5°C.

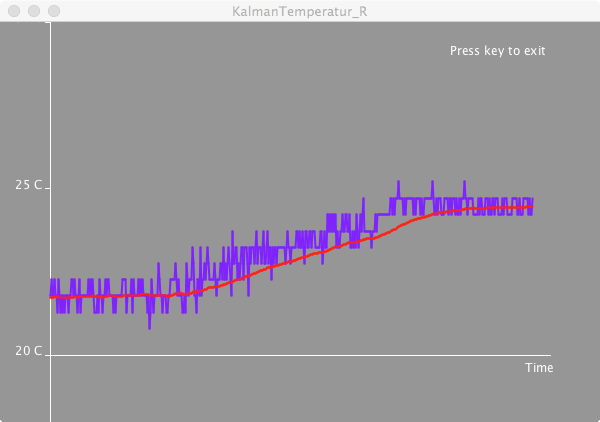
Changing the parameters \(\sigma_P\) and \(\sigma_M\) influence how quickly the filter reacts to changes. Here is an example where I briefly touch the temperature sensor with the above parameters. The time axis in those screen shots is about 6 seconds.

I have to do a bit more reading on the Kalman filter. It appears to be an immensely powerful tool to extract the signal from the noise. Well, it helped to put a man on the moon.

Code

This is the Processing and Arduino code I used in this post. You may have to change the port number in line 28 to your own settings.