Phase plane analysis in R
The forthcoming R Journal has an interesting article about phaseR: An R Package for Phase Plane Analysis of Autonomous ODE Systems by Michael J. Grayling. The package has some nice functions to analysis one and two dimensional dynamical systems. As an example I use here the FitzHugh-Nagumo system introduced earlier:
\[
\begin{aligned}
\dot{v}=&2 (w + v - \frac{1}{3}v^3) + I_0 \\\\\\
\dot{w}=&\frac{1}{2}(1 - v - w)\\\\\\
\end{aligned}
\]
The FitzHugh-Nagumo system is a simplification of the Hodgkin-Huxley model of spike generation in squid giant axon. Here \(I_0\) is a bifurcation parameter. As I decrease \(I_0\) from 0 the system dynamics change (Hopf-bifurcation): a stable equilibrium solution transform into a limit cycle. Following Michael’s paper, I can use  Yet, I was a little surprised that the paper didn’t make any references to the XPPAUT software by Bard Ermentrout, which has been around for many years as tool to analyse dynamical systems.The GUI to the software itself gives many more options to analyse dynamical systems, including an interface to the popular bifurcation program AUTO. A good tutorial with the FitzHugh-Nagumo model was given by Mathieu Desroches at the ICS summer school 2012.Of course I could use XPPAUT as a pure integration engine from R as well:
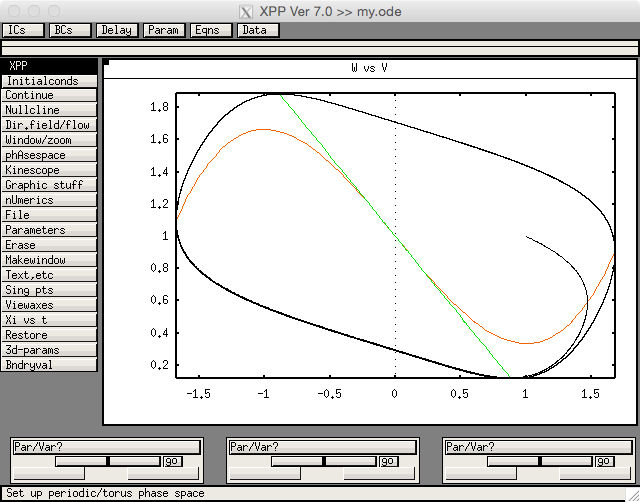
Yet, I was a little surprised that the paper didn’t make any references to the XPPAUT software by Bard Ermentrout, which has been around for many years as tool to analyse dynamical systems.The GUI to the software itself gives many more options to analyse dynamical systems, including an interface to the popular bifurcation program AUTO. A good tutorial with the FitzHugh-Nagumo model was given by Mathieu Desroches at the ICS summer school 2012.Of course I could use XPPAUT as a pure integration engine from R as well:
 Considering that R started as a tool for statisticians it has made a remarkable journey; here competing with more traditional engineering tools like Matlab with MatCont or special software like XPPAUT. If someday, someone would find the time and motivation to write an interface to AUTO then R would indeed be a very good environment for the analysis of dynamical systems.
Considering that R started as a tool for statisticians it has made a remarkable journey; here competing with more traditional engineering tools like Matlab with MatCont or special software like XPPAUT. If someday, someone would find the time and motivation to write an interface to AUTO then R would indeed be a very good environment for the analysis of dynamical systems.
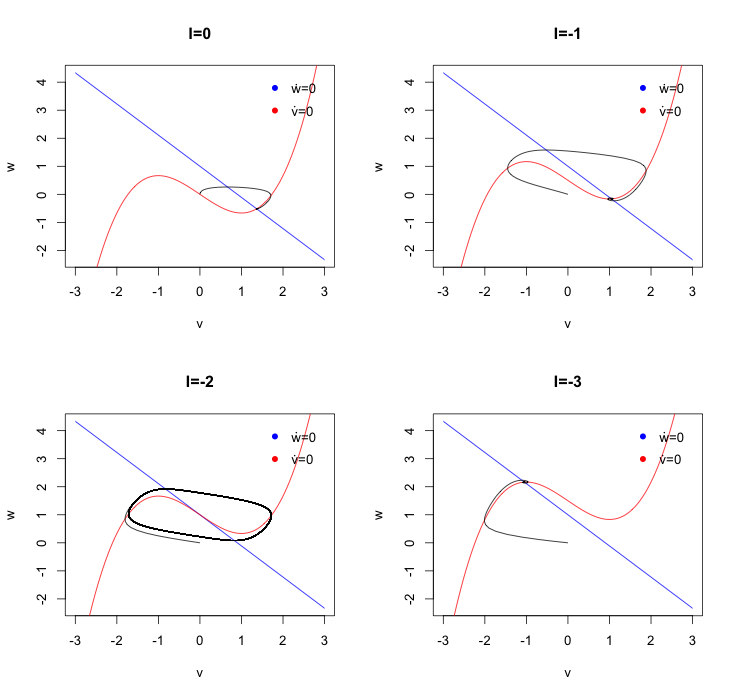
phaseR to plot the velocity field, add nullclines and plot trajectories from different starting points. Here I plot the FitzHugh-Nagumo system for four different parameters of \(I_0\) and three different initial starting values. The blue line show the nullcline of \(w\) i.e. \(\dot{w}=0\), while the red line shows the nullcline of \(v\). For \(I_0=-2\) I can observe the limit cycle.
 Yet, I was a little surprised that the paper didn’t make any references to the XPPAUT software by Bard Ermentrout, which has been around for many years as tool to analyse dynamical systems.The GUI to the software itself gives many more options to analyse dynamical systems, including an interface to the popular bifurcation program AUTO. A good tutorial with the FitzHugh-Nagumo model was given by Mathieu Desroches at the ICS summer school 2012.Of course I could use XPPAUT as a pure integration engine from R as well:
Yet, I was a little surprised that the paper didn’t make any references to the XPPAUT software by Bard Ermentrout, which has been around for many years as tool to analyse dynamical systems.The GUI to the software itself gives many more options to analyse dynamical systems, including an interface to the popular bifurcation program AUTO. A good tutorial with the FitzHugh-Nagumo model was given by Mathieu Desroches at the ICS summer school 2012.Of course I could use XPPAUT as a pure integration engine from R as well:
 Considering that R started as a tool for statisticians it has made a remarkable journey; here competing with more traditional engineering tools like Matlab with MatCont or special software like XPPAUT. If someday, someone would find the time and motivation to write an interface to AUTO then R would indeed be a very good environment for the analysis of dynamical systems.
Considering that R started as a tool for statisticians it has made a remarkable journey; here competing with more traditional engineering tools like Matlab with MatCont or special software like XPPAUT. If someday, someone would find the time and motivation to write an interface to AUTO then R would indeed be a very good environment for the analysis of dynamical systems.Session Info
R version 3.1.2 (2014-10-31)nPlatform: x86_64-apple-darwin13.4.0 (64-bit) locale:n[1] en_GB.UTF-8/en_GB.UTF-8/en_GB.UTF-8/C/en_GB.UTF-8/en_GB.UTF-8 attached base packages:n[1] stats graphics grDevices utils datasets methods n[7] base other attached packages:n[1] phaseR_1.3 deSolve_1.10-9 loaded via a namespace (and not attached):n[1] tools_3.1.2Citation
For attribution, please cite this work as:Markus Gesmann (Nov 04, 2014) Phase plane analysis in R. Retrieved from https://magesblog.com/post/2014-11-04-phase-plane-analysis-in-r/
@misc{ 2014-phase-plane-analysis-in-r,
author = { Markus Gesmann },
title = { Phase plane analysis in R },
url = { https://magesblog.com/post/2014-11-04-phase-plane-analysis-in-r/ },
year = { 2014 }
updated = { Nov 04, 2014 }
}