Simulating neurons or how to solve delay differential equations in R

I discussed earlier how the action potential of a neuron can be modelled via the Hodgkin-Huxely equations. Here I will present a simple model that describes how action potentials can be generated and propagated across neurons. The tricky bit here is that I use delay differential equations (DDE) to take into account the propagation time of the signal across the network.

My model is based on the paper: Epileptiform activity in a neocortical network: a mathematical model by F. Giannakopoulos, U. Bihler, C. Hauptmann and H. J. Luhmann. The article presents a flexible and efficient modelling framework for:

• large populations with arbitrary geometry
• different synaptic connections with individual dynamic characteristics
• cell specific axonal dynamics

In its simplest form, for one self-coupled neuron or you could regard this as the synchronised case of several neurons, I have: \[ \begin{aligned} \frac{du}{dt}=&\alpha (-u(t) + q g(v(t-T)) + I) \\ \frac{dv}{dt}=&C (w(t)+v(t)-\frac{1}{3}v(t)^3) + \gamma u(t) \\ \frac{dw}{dt}=&\frac{1}{C}(a-v(t)-bw(t)) \\ g(v) = & \frac{1}{1 + \exp(-4v)} \\ \end{aligned} \] The variable u describes the total post-synaptic soma potential, which is the sum of all incoming signals v. The membrane potential v arrives via the dendrites after a time delay of T and is either exhibitory (q > 0) or inhibitory (q < 0). It is transformed from a pre to a post-synaptic signal by the monotonically increasing function g.

The membrane potential v itself is modelled by FitzHugh-Nagumo differential equations. They can be regarded as a simplified version of the higher dimensional Hodgkin-Huxely model.

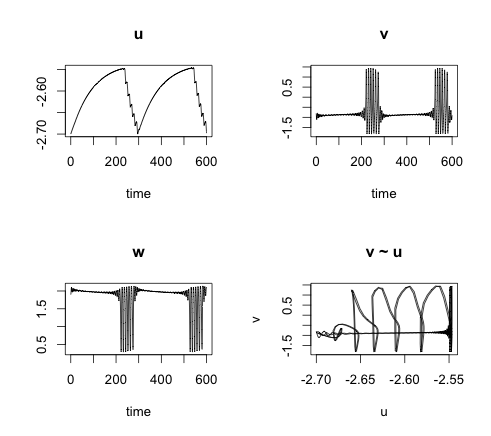
The soma potential u is for \(0 \lt\alpha\ll 1\) on a much slower time scale than v. Thus, with u treated as constant we can analyse the FitzHguh-Nagumo (FHN) system. The FHN system has an interesting bifurcation behaviour, using u as a parameter. For certain values of u the system has a stable equilibrium; increase the value of u and the FHN system will go through a Hopf-bifurcation and periodic solutions with a limit cycle attractor appear (the neuron spikes).

Combining the FHN model with the soma potential u provides a model which is most fascinating. In my example the resting membrane potential slowly increases the soma potential until the FHN system goes through a Hopf-bifurcation resulting in periodic spiking (bursting), which in in itself pushes the potential u down, eventually causing the neuron to rest again.

Introducing the time delay T not only makes the model more realistic, it allows me to control the length of the bursting phase as well. A more detailed examination of the system is presented in Bursting activity in a model of a neuron with recurrent synaptic feedback by F. Giannakopoulos, C. Hauptmann and A. Zapp.

To simulate and analyse the model in R, I use the deSolve package, maintained by Thomas Petzoldt. The package comes with an excellent vignette and the DDE solver dede. The function dede is actually easy to use, once you get your head around it. Here is an example of the above model:

R Code